How about a real Galactic survey?

kw: ideas, surveys, astronomy

OK, yesterday I reviewed a book about the Sloan Digital Sky Survey, whose primary goal was to obtain the spectra of a million galaxies scattered through redshift space. An additional harvest was the spectra of about half a million stars located in our Galaxy, which has led to a flurry of additional discoveries.

This complemented earlier surveys, particularly ESA's Hipparcos mission, which from 1989-1993 obtained highly accurate positions and parallaxes (distances) for more than 118,000 stars and slightly less accurate positions and parallaxes for another 2.5 million stars. That represents about 0.02% of the stars in the Galaxy, primarily located within a few thousand light years of the Solar System. SDSS did not pursue parallaxes specifically. ESA (the European Space Agency) plans a mission called Gaia, to be launched in 2012, which is intended to map a billion (10⁹) stars of magnitude 20 and brighter.

Let's consider a space mission that could map all of the roughly one trillion (10¹²) stars, obtaining geometric parallaxes throughout the Galaxy. Firstly, it needs a larger baseline.

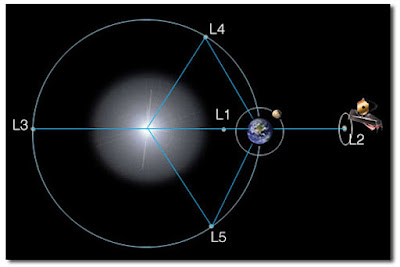In this NASA image, the Lagrange points are shown for Earth's orbit about the Sun. NASA's WMAP probe is intended to park in the L2 point. Although it is unstable in the long term, staying near this location is easy, needing correction at rare intervals. The Gaia probe is intended to use the same region.

For getting parallaxes, the L2 location, located 1.5 million km farther from the Sun, is only slightly better than a telescope in Earth orbit. In a half year, the baseline for parallax determination is 300 million km. Getting more precise distance measurements requires ever-more-finicky angular measurements. For stars that are moving too fast, the difficulty is compounded. Having two probes a suitable distance apart allows simultaneous measurement of each star's position from two angles.

One light year is a little less than one-third of a parsec, so named because a parallax of one arc-second places a star at 3.26 light years away. A measurement with an accuracy of 1"/1000, or one milli-arc-second (mas) can provide a distance with reasonable accuracy out to about 100 parsecs, and with poor accuracy at distances approaching 1000 parsecs, or 3,260 light years. It takes accuracy in the range of a micro-arc-second (µas) to reach across the Galaxy, about 30,000 parsecs. By the way, the parsec is defined for a baseline of 1 AU, but in a half year the earth crosses a baseline of 2AU.

Suppose, instead of utilizing Lagrange points related to Earth's orbit, we use both L4 and L5 along the orbit of Uranus? The baseline is thus much longer! Uranus is 19.19 AU from the Sun (2,871 million km). The distance from L4 to L5 is 33.2 AU, providing an advantage of 16.6 over Earth-orbit-based parallax measurements. At a distance of 30,000 parsecs, the parallax is about 0.55 mas, a comfortable number using today's technology. Thus the entire Galaxy, including the globular clusters, and even the Magellanic Clouds, can be mapped with high precision.

The problem remains that the Solar System is located in the plane of the galactic spiral, about 2/3 of the way out to the edge. The central bulge and the incredible amounts of dust there and in parts of the disk will forever block our view. Much of the dust can be pierced by using farther infrared light, in the 2-3µ range. But from this location, some portions of the Galaxy will forever remain out of view.

Balancing this, there will be much less interference from dust in the inner Solar System, which can be seen from Earth as the Zodiacal Light. Light scattered from this dust is nearly all confined to inward of Jupiter. From Uranus, the Sun is 360 times dimmer, as well, so any dust remaining in "Uranus space" will likely be at least 6-8 magnitudes fainter, allowing very faint stars to be detected and measured. A white dwarf with an absolute magnitude of about 16 dims to apparent magnitude 26 at a distance of only 1,000 parsecs. At 30,000 parsecs it is dimmed, by distance alone, by another 7 magnitudes, to 33. A 33^d magnitude star is barely detectable from "Earth space", but should be nice and clear when seen from Uranus orbit.

I have read of proposals to have a mission called TAU, for Thousand AU's. The idea is to place a telescope at that great distance, for measuring parallaxes in a wide band surrounding the plane that bisects the baseline. This has several drawbacks. With current technology, getting the probe into place, and then stopping its forward momentum (should we wish to) would take a couple of centuries. Getting probes to Uranus L4 and L5 would still be substantial, roughly a decade, unless rocket technology improves considerably.

Also, the data transit time to or from TAU would be about 5.8 days. Data transmission to and from Uranus orbit takes about 2.6 hours, and signal strength is much greater for a given radio power. All in all, taking advantage of the L4 and L5 "platforms" near Uranus has great advantages for stellar mapping throughout the Galaxy.