The usual is less usual than we think

kw: analysis, statistics, black swans, statistical distributions

Alternative Title: Thousand-year Floods Occur Too Often

Just to set expectations ahead of time: The aim of this article is to analyze activity for a stock in the U.S. stock market. However, the phenomena of interest here apply in numerous areas, including flood control, a fun place to begin.

This picture shows the Sorlie Bridge linking Grand Forks, ND with East Grand Forks, MN, during the flood of 1997. It's what happens when you design for a 100-year flood, and it has been 170 years since the last big flood. The peak flow was only 5% greater than the design criterion.

What would a 1,000-year flood look like? Sooner or later it'll happen. Some interesting statistics are involved.

Here we have a log-Pearson plot of gauged "floods" on a river in Australia. AEP is "Annual Exceedance Probability". I was taught how to make such plots during a summer project in graduate school. The data are the highest flow recorded every time the river overflows its inner banks. There are 46 such events charted here. I infer from the rightmost datum that the record goes back about 80 years. A "flood" as thus defined will happen every year or two.

Extending the coordinates of this chart I estimate that a 1,000-year flood would have a peak flow of between 350 and 400 on the scale shown (I infer m³/s; in ft³/s: 12,000-14,000), not quite twice the flow of a 100-year flood.

Quantitative hydrology doesn't extend back even 200 years. How can we validate the use of log-Pearson analysis in extrapolating for 1,000-year floods? There are also at least two other analysis methods in use. How could we validate any of them?

Nearly forty years ago, a fellow student of mine in graduate school worked out such a validation, for at least one "creek" in the Black Hills area. In this view from Google Maps, the creek mouth is off the left. The image width is about a quarter mile.

The boulders seen here are not glacial erratics. The student, Bill, measured lichen patches on hundreds of the boulders, choosing only those larger than he was. He was able to discern, by the size of the largest patch of a certain kind of lichen on each boulder, when they were last tumbled down the creek and washed out onto the plain, sometimes as far as a couple of miles. He determined the outwash area for twenty large floods from that creek. I saw a map he made of those outwash areas.

References on lichenometry helped him obtain approximate dates for the floods. All had occurred in the past 5,000 years. As a student of hydrology, he was able to determine the flow volume needed to move a car-size boulder a half mile to a mile from the creek mouth. Here's the kicker: a chart of historical hydrology measurements on that creek indicate that every one of the twenty floods was at least a 1,000-year flood. But they were actually something like 250-year floods! (or, actually, scattered out from 250 years and upward.) Such data didn't fit into the historical analysis. To be clear about what follows, the log-Pearson analysis is not related to the Normal Distribution, nor to Lognormal statistics.

Statistical analysis in many areas depends heavily on the Normal Distribution, AKA Gaussian. As it happens, this is frequently a very good model. However, even the textbook example, human height, isn't as "normal" as it might seem. In this blog post by John D. Cook, he shows that extremes of height and of shortness are not well predicted by a normal distribution with a standard deviation of 2.5 inches, the criterion that fits well for about 95% of the data for men and for women (which must be analyzed separately). By that measure, there should be no more than one man taller than seven feet, or shorter than 4'-5", nor one woman taller than 6'-9", or shorter than 4'-1", among our entire world population of more than 7 billion. But the NBA is full of seven-footers (more than 40, as counted in 2018), and there are numerous "little people", particularly in entertainment, ranging from four feet down to just above two feet tall. The shortest adult woman on record measured nineteen inches. Data such as these fit better a "fat tailed" distribution, for which more extreme values are more frequent than a Normal analysis would predict.

For events such as floods, it is likely that the excess frequency of extra-large floods is due to a different climate regime from the usual. For height measurements on people, different populations with distributions account for some of the "excess" variation, while medical issues such as glandular gigantism or dwarfism also account for some. These kinds of considerations indicate that we need to study a broader scope of phenomena. If an analysis doesn't include everything relevant, our model is incomplete. But what of "surprises" in a data set that is thought to be well-behaved?

These are examples of black swans. I reviewed The Black Swan by N.N. Taleb thirteen years ago. The book's theme is that "uncommon" events aren't so uncommon. He applied findings such as these to investing. You may recall there had been a significant bear market a few years earlier, starting in 2000. The one that followed the book by a year (2008-09) made Taleb look like a prophet. Now we are in the middle of another one.

One claim in The Black Swan is that daily moves on stock issues follow a Cauchy distribution. It is described as the ratio of the sine of one uniform random variable divided by the cosine of another. Mathematically, that is the tangent of a uniform random variable over the interval [-π/2, π/2], but not including the end points, for which its value is infinite. The Cauchy distribution is typically described as a tangent function over the half circle.

That was something I could test. The Cauchy distribution is very fat-tailed or, viewed another way, it middle part very skinny compared to a normal distribution. It looks like this. We'll see how a normal curve looks in a moment.

Does the distribution of daily closing values of stocks in the market look like this? I chose the most stable stock in America, AT and T, to test this. I used data for the past 37 years (everything available through Yahoo! Finance). I used what they call "Adjusted Close", which factors in the values of stock splits and dividends. I analyzed the entire period, and two sub-periods, the ten years from 1/1/1984 to 12/31/1993 and the two years from 1/1/2018 to 12/31/2019. Note: I'll call this company "ATT" to avoid the ampersand, which is not well behaved in HTML text.

This is the shape of the distribution of daily moves, expressed in percent, and two normal distribution curves. As the legend indicates, the blue curve shows the recent two years, the green curve shows the early ten years (which includes the crash of 1987), and the red curve shows all 37 years. The dashed magenta line is a normal curve with the same standard deviation as the 37-year curve, and the thin black line is a normal curve that fits the bulk of the data, but not the tails. I hope you can see that a normal curve looks broader than the Cauchy curve in the chart just above. The range -10% to +10% doesn't quite encompass all the data; there are three data points further to the right and one further to the left…out of nearly 9,200 daily motions.

It may take some peering, but it is also visible that the black curve outside the range [-2%,+2%] lies below the red, green, and blue curves. Those small amounts are the "fat" in the fat tails of those three distributions. Their very similar shapes also illustrate why I call ATT so stable. Through thick and thin it preserves a certain character of daily responses to market pressures. I do not intend to compare ATT to another stock here; that is for another day, another post.

It will perhaps be easier to see the implications of these data by looking at cumulative distribution functions (CDF's).

The x-axis of this chart is in units of standard deviation. The straight, black dashed line shows how a normal distribution would plot as a straight line. The ATT data going above at the left and below at the right are the fat tails of their distribution.

Looking at the two charts above, one may suspect that the ATT CDF is not as fat-tailed as a Cauchy distribution. The next chart shows this:

The x- and y- axes are in different units because I didn't normalize them. However, the very flat shape of the curve between -2 and +2 standard deviation units shows that the tails are much fatter than those for the ATT data.

Stock market motions, at least for this stock, are thus not as extremely variable as a Cauchy-distributed function.

I must at this point make an aside regarding lognormal distributions. My geologic background as an undergraduate emphasized sedimentology. One tool used to study sediments such as a sandy soil is to shake a sample through a stack of sieves and make a frequency distribution of the result, by weight. The sieves are carefully crafted to separate particles, at each step, that are 1.414 (i.e., √2) smaller in diameter. The frequency distribution so produced is a lognormal analysis. A frequency plot for a well-developed sediment from a single source will look like a normal curve, except that the x-axis is the logarithm of particle diameter. Over the years I found that many natural phenomena that have a wide range are lognormally distributed. We can check for lognormality by charting on log-probability coordinates.

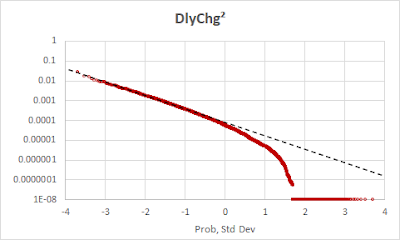
I decided to see if the distribution of stock price daily moves might be related to a lognormal distribution. I squared the ATT data; thus all the results are positive, no longer both up and down. This is a CDF of the result, with the vertical axis logarithmic.

If the data closely followed the black dashed line, they would be lognormally distributed. The data charted at 1E-08 were actually zero, but that cannot be shown on a log-probability chart. What is the big dip leading up to them? This is a consequence of the size of a penny! I call it the "penny effect". During part of the interval stocks were traded only in increments of 1/16 of a dollar, then in increments of certain fractions of a penny, and since then in whole cents.

If the stock is trading for $10, and the next day the closing price is $10.01, the difference between the two is 0.1%, or 0.001 (10.01/10.00 - 1). Squaring this produces 0.000001. When the adjusted closing price is closer to $5, as it was in the early 1980's, a penny difference is 0.002, which squares to 0.000004. This, and a psychological effect that many people avoid prices so close to a prior day's price all led to the drop-off seen here. Since this is a pretty good fit to lognormality, other than the "penny effect", I call the distribution of stock price moves "Square Root of Lognormal."

Let's look at the squared Cauchy data. It is a continuous distribution with no pennies to worry about, so there is no drop-off. But the data are not lognormal either. The black dashed line is lognormal. The tails of this distribution are fatter than the tails of a lognormal distribution, much fatter. From experience I can tell you, that's pretty hard to do!

It so happens that this distribution is ill-behaved no matter how you transform it. In terms only a statistician could love, the Cauchy distribution has no "moments". That means that trying to measure anything other than its average value is meaningless. You can calculate a standard deviation for it, for example, but it has no meaning.

How does this relate to black swans? In stock market terms, if the daily moves were truly distributed according to Cauchy statistics, huge moves would be even more common than they are. However, the Square Root of Lognormal function that daily prices do seem to follow is not nearly so extreme, but it does have many more large moves, up or down, than a normal model would lead someone to believe. The standard deviation of the ATT data is about 1.5%. That means that, as seen in the chart above titled "Daily Change, all", none of the daily price moves should have been outside the bounds of [-4%, +4%]. However, on 250 occasions, a daily move was outside this range. That's only 2.7% of all the data. However, 250 times in 37 years means that six or seven times yearly, ATT's stock price moved by more than a normal model would predict is even possible during a run of nearly 9,200 market days.

Conclusion? To better predict the range of variation for a particular stock, list the daily moves over a period of a few years, square them, and plot as a CDF. From this you can determine a log-standard deviation, and its square root will yield a much better parameter of variation for the stock's behavior.

This last chart is a frequency diagram of the squared data for ATT, and the horizontal axis is logarithmic. The blip at the left is the "penny effect". Other than that, and a bit of skew, it looks a lot like a normal distribution; the choice of axis shows its affinity to a lognormal distribution.

Whether this will lead to a more robust way to set an investment strategy is anyone's guess!