It takes big eyes to see fine detail, part 2

kw: musings, physics, light, visibility

In the prior post I explained that larger eyes can see, and larger cameras can record, more detail from a particular object or scene. Briefly, the size of the smallest spot that can be produced by a diffaction-limited lens has a radius expressed by the Airy formula,

x = 1.22 λf/d

Given an effective wavelength (λ) for "average" visible light of 0.6µ, this formula tells us that the radius x of the smallest spot (on film or digital sensor) that the lens can make depends only on its focal ratio f/d. A small lens with a short focal length can cast an image on a only a small area, comparable to the lens-to-sensor distance. A larger lens at a greater distance from the sensor can cast a useful image on a sensor of larger area. Since the spot size, which limits the useful pixel resolution, is the same for both lenses, the larger lens will capture more detail from the object being viewed or imaged.

Continuing with visible light, let us consider how to see finer and finer detail in extreme close-up mode. When the lens gets closer to the object than it is to the sensor, things get a bit more complex, but only a bit. In the diagram below, the small "F" on the left is being magnified by a lens to produce a real image, shown as a larger "F".

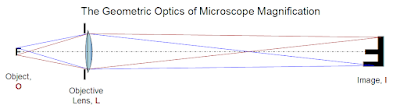The real image to the right can be seen if you put your eye a suitable distance further to the right, and if you put camera film or a digital sensor in the real image's location, the "prime focal plane" it will record the image. In the arrangement shown, the real image is four times the size of the object.

To analyze the detail we might be able to record, there are two regions of interest:

• The Object-to-Lens distance and Lens diameter establish the Objective focal ratio, which determines the smallest detail on the Object that can be imaged. In microscopy, this is usually expressed as its inverse, the Numerical Aperture, or N.A. For this diagram, the Objective focal ratio is 2, so the N.A. is 0.5. Using the formula above, the smallest detail seen will have a radius of 1.22x0.6µx2 = 1.46µ.
• The Lens-to-Image distance and Lens diameter establish the Image Focal Ratio, which determines the effective pixel resolution of the system. The magnification here is 4, meaning the lens-to-image distance is 8 times its diameter, so this is a f/8 system. The blur circle is thus 1.22x0.6µx8 = 5.86µ, or about 6µ in radius.

To take good advantage of this system, a digital camera sensor needs pixels 6µ x 6µ or smaller. Note that in magnifying the image, the lens has also magnified the blur circle by an equal amount. This is a 4x objective. A 40x objective will magnify the blur circle by 40x, to about 60µ if the objective focal ratio is f/2. Viewing with the eye and recording with a sensor will both need some mediation.

How much detail can the human eye see? People who are not nearsighted typically look at something no closer than 10" (250mm). Normal vision has an angular resolution (at the point of attention) of about a minute of arc, which means we can resolve items no finer than 1/3,500 of the distance from the eye. Vision called 20/20 is based on resolution closer to 1/1,000, or about 3.5 minutes of arc. Photographs printed at your local drug store have a resolution of 200 pixels per inch, or 8/mm. Held at a close distance, where they still "look pretty good", the finest details are about 1/2,000 the distance to the eye. Let us use this ratio to understand what we need to do to see everything the objective lens above is putting into the real image it presents to us.

If you place your eye ten inches from the real image, you can see it. The smallest details visible to you will be about 1/8mm or 1/200 inch apart; 1/8mm is 125µ. The original 4x system is producing a real image with details as small as about 6µ, so a lot of the detail in the image is wasted.

That is why the compound microscope has an eyepiece. A 10x eyepiece is placed one inch (25mm) from the real image and lets you see the image ten times larger. In this instance, you can now see details in the image as small as 12.5µ. To see "everything that is there", you need a 20x eyepiece, which lets you see 6.25µ details, which is getting close. At that point, the effective magnification is 80x. So how do microscopes with effective magnification of 1000x or so work?

First, we have to get a lens that has a lot smaller Objective focal ratio, smaller than f/1. It was discovered about a century ago that there is a point inside a glass sphere for which spherical aberration was nullified. Simply speaking, that means an easy-to-produce lens can magnify a lot. To get the object "inside" a spherical lens, one side of the sphere is ground flat, and an immersion medium such as oil is used to "extend" the lens so it surrounds the object:
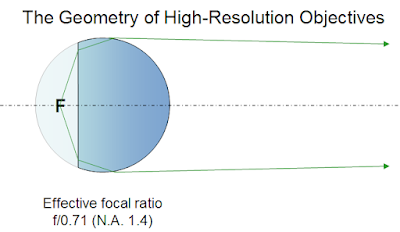Ratios as low as f/0.55 are possible, but f/0.71 is most common with glasses that need minimal color correction. At f/0.71, the Rayleigh criterion at 0.6µ means that detail on the Object can be seen as small as 1.22x0.6µx0.71 = 0.52µ. What magnification is then possible? Recall that the 1/2,000 criterion means that human eyes can see 1/8mm or 125µ. 125/0.52 = 240x. That is the maximum "useful" magnification using visible light.

Most high-power oil-immersion lenses are designed to provide a real image 100x larger than the area of the object being examined. So when you use a 10x eyepiece, you're seeing that area magnified 1,000x. However, if you examine the image critically (I have done so), you will realize that the edges between light and dark objects do not appear knife-sharp. Try a lower-power eyepiece: 5x looks a lot sharper, though of course everything appears smaller. You can't get 2.5x eyepieces, but if you could, the image you see would be well matched to the ability of your eye. The value of looking at the larger, blurrier image is that you can scan it more effectively for the subtle details, which might be missed at a lower magnification. As a reference, an E. coli cell has a diameter near 2µ and a length of about 5µ, so these critters look pretty small even at 1,000x.

A bit of extra resolution can be had by using a shorter wavelength. I've used, with little explanation, an effective wavelength of 0.6µ. That is the effective wavelength for incandescent light, which is rather orange, though we get used to feeling that it is "white enough". But if we throw away most (not all) of the red-orange light with a filter, we'll have a bluish light that is also "white enough" but has a shorter effective wavelength. My microscope came with a "daylight" filter that shifts the effective wavelength to about 0.48µ. With this filter, the ultimate resolution of the 100x objective is not 0.52µ but 0.42µ, allowing a magnification at maximum sharpness of 300x, and quite a bit more detail is then visible at 1,000x.

A slightly mathematical note to finish this portion: Microscopes have been standardized for decades at a 160mm "tube length", which fixes the distance between the real image and the objective lens at 160mm. The actual size of the microscope depends on the way the lenses are attached. A f/0.71 objective lens (N.A. 1.40) thus has a distance from the object (the microscope slide) of 1.6mm and a diameter of 2.25mm. The lens-to-image focal ratio is 160/2.25 or f/71 (100 times f/0.71). With my blue filter in place, the pixel size of the real image is 42µ (100 times 0.42µ). If I put a digital camera sensor in the focal plane, where the real image is, a lot of its resolution will be wasted. That is why microscopes set up for photography use a relay lens that shrinks the image, usually by a factor of 8, so that it is well-suited to recording by a sensor whose pixels are in the 5µ-10µ range.

These are the limits to seeing fine detail with visible light. Though I'd intended to explore shorter wavelength light (and other radiations), this post is long enough already.