To my summer math students
We use Differential Calculus to produce the D operator. The D operator acts on a function to produce another function that expresses the slope of the first function. We'll sneak up on it by way of example, using this graph.
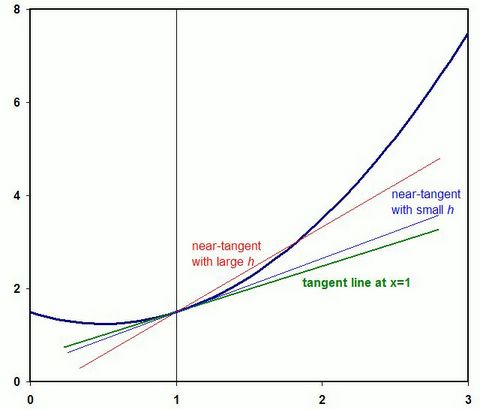
Approaching the Tangent

We want to find the slope of the black curve where the x coordinate is 1.0; a line having this slope is tangent to the curve as shown by the green line. If we know the function y=f(x) that produced the curve, we can estimate the slope by figuring y at x=1, then choosing a nearby point x+h, or 1+h in this case, and figuring a new y=f(x+h). Then we can take the difference in y and divide by the difference in x (which is h) to get an approximate value for the slope. The formula is thus:
slope ≈ [f(x+h) - f(x)] / h
If h is relatively large, the estimate will be less accurate than when h is small. The red and blue lines on the graph illustrate this. However, if h is very small, we will find that rounding error causes some loss of precision also.
For the curve above, here are estimates of the slope calculated for different values of h:
h = 0.500, slope = 1.500
h = 0.250, slope = 1.250
h = 0.125, slope = 1.125
This curve was chosen to make it easy to show that the slope approaches 1 when x=1 and h approaches zero. We express this situation with a limit statement:
slope = lim{h→0} [f(x+h) - f(x)] / h
The beauty of this expression is that for many functions, the algebra works out so that an h in the numerator cancels out the h in the denominator, so you can then set h to zero to get a new function that expresses the slope you want, for any value of x. Here is how it works for a simple monomial. We'll use y', or "y-prime", to refer to the new function that was derived from the original function.
y = x3
y' = lim{h→0} [(x+h)3 - x3] / h
Now, (x+h)3 = x3 + 3x2h + 3xh2 + h3
Thus [(x+h)3 - x3] / h = [3x2h + 3xh2 + h3] / h
Note that every term in the numerator now contains h, so we can cancel to get
y' = lim{h→0}[3x2 + 3xh + h2] = 3x2
So we assert that the slope of the function y = x3 is y' = 3x2 at every point. We'll explore more polynomials and their derivatives, or slope functions, in a later post.
Now, a word on nomenclature.
The differential formula is so called because it calculates a difference, though it reduces the range of that difference to zero. It can operate on a point to produce a slope at that point. But mainly, it operates on a function to produce another function. The second function is derived from the first, so it is called its derivative. For many functions, the derivative also has a derivative, called the second derivative of the first function.
There are three common ways to express the operation and to label the derivative. These arose because several different people developed the method, and each invented his own symbolism. They are retained because they are each useful in various situations.
Prime notation: the derivative of function y is y', or the derivative of f(x) is f'(x). These are pronounced "y prime" and "f prime of x". The second derivative is shown with a double prime: y" or f"(x), pronounced "y double prime" and "f double prime of x".
d/dx notation: the derivative of function y is dy/dx, or that of f(x) is df(x)/dx . These are pronounced "d y d x" and "d f of x d x". The second derivative is shown by an exponent; this makes this notation more useful for third and higher derivatives. d2y/dx2 and d2f(x)/dx2 are pronounced "d squared y d x squared" and "d squared f of x d x squared."
D notation: the derivative of function y is shown as either D(y) or Dx(y), depending on whether one needs to explicitly show that the derivation is with respect to x (it could be with respect to t, for example, instead). Higher derivatives are shown as an exponent on the D only. This notation is seldom used with a function shown as f(x), because of multiple parentheses.
For each notation, the formal operator is the prime, the d/dx, or the D, respectively.
No comments:
Post a Comment